この記事の目的

RNN, LSTMの理論を理解し、Kerasで実装できるようにするために、理論部分をまとめた記事。

0. 通常のNeural NetworkやConvolutional Neural Networkの問題

これまでNNやCNNは入力サイズが固定だった。そのため、毎回同じ入力をするしかなく、時系列情報を入力させることができなかった。

RNN・LSTMは、入力を可変にして過去の出力結果も学習に利用できるようにしたニューラルネットワークのモデルである。

RNNの基本的な構造は、「現在入力値と前回の出力値を合計し、活性化関数としてtanhを適用して出力とする」という流れ。

上図でいうと、現在の入力が $x_t$ となり、前回の出力値が $h_{t-1}$ となる。

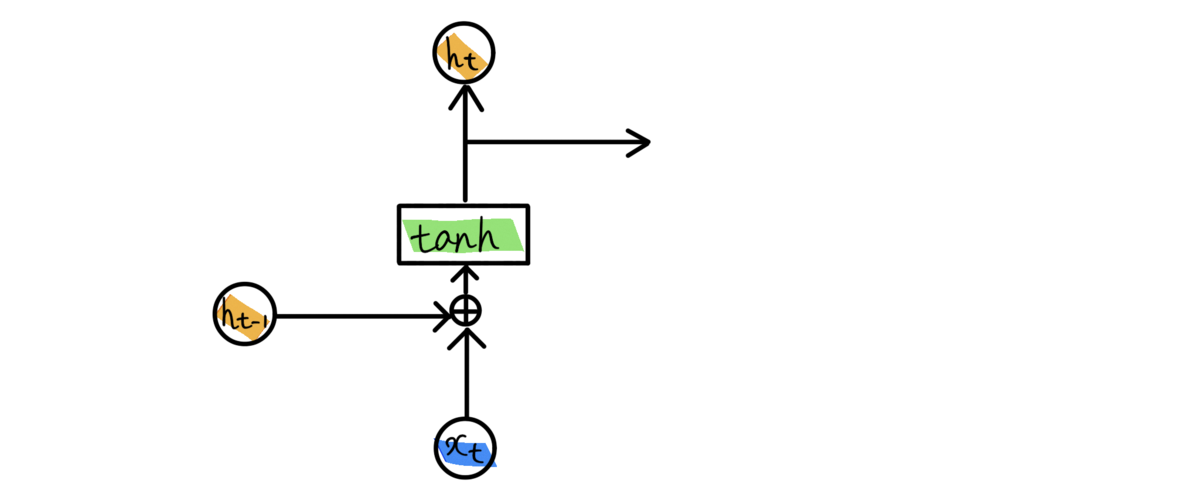
隠れ層では活性化関数としてtanhが一般的に選ばれる。

数式で表すと、
$h_t = tanh(x_t + h_{t-1})$
となる。

tanhは $x_t$ と $h_{t-1}$ の和を-1〜+1の範囲に正規化する。

tanhが選ばれる理由は、２次微分の減衰がかなりゆっくりとゼロになり勾配消失問題が起きにくいため。

過去データに対する重みが発散、消失する問題のこと。下記サイトの解説が分かりやすい。

発散・消失する理由は、最初の方のレイヤーの逆伝播計算時に、何度も重みwとシグモイドの微分を掛け合わせるからである。

シグモイド関数の微分は0~0.25の範囲である。そのため、重みwが1以下だったら、最大でも　 $w*σ'(z)= 1 * 0.25 = 0.25$ 　となるので、0.25を繰り返し乗算することで、勾配がほぼ0になってしまう。これが勾配消失と呼ばれる理由。

また、重みwが0.25をかけたらかなり大きくなる値（100とか）の場合、0 ~ 0.25 × 100 = 0 ~ 25 の範囲になるため、最悪25×25×25×…となってしまい、勾配が発散してしまう、勾配爆発問題が起きる。（これはバイアスでも同じ話）

このように最初のレイヤーの重みとバイアスがかなり小さくなってしまうことにより、新たな入力値を学習しようとしてもかなり小さくなってしまうため、モデルの学習に寄与しなくなってしまう。

RNNでも数十ステップの短期依存(short-term dependencies)には対応できる。しかし、1000ステップのような長期の系列になると、tanhを使って上記の問題を和らげるとはいえ、無視できないくらい勾配が小さく（もしくは大きく）なってしまい、上述の勾配消失（爆発）問題が発生する。

この対処法としては下記のようにいくつかある。

中でも４番目に記載した「LSTM」では過去のデータを保持する仕組みを使って、勾配消失問題を回避している。

この続きはcodocで購入